6021. Мега Инверсии
Верхнюю оценку n2 в алгоритме сортировки
получить легко: достаточно найти два элемента, стоящих в неверном порядке, и
поменять их местами. Конрад задумал в алгоритме взять не два, а три стоящих не
в правильном порядке элемента. То есть возьмем три элемента ai > aj > ak
у которых i < j < k и переставим их
в порядке ak, aj, ai. Если в исходном алгоритме количество шагов
ограничить максимальным числом инверсий n
(n – 1 ) / 2, то Конрад в своей
версии алгоритма также хочет ограничить этим значением количество переставляемых
троек. Напишите программу, которая подсчитает количество таких троек.
Вход. Первая строка
содержит длину последовательности n
(1 ≤ n ≤ 105).
Следующая строка содержит последовательность чисел a1, a2,
..., an (1 ≤ ai ≤ n).
Выход. Вывести
количество инвертированных троек.
|
Пример
входа |
Пример
выхода |
|
4 3 3 2 1 |
2 |
РЕШЕНИЕ
структуры
данных – дерево Фенвика
Анализ алгоритма
В ячейках pref[j] для каждого значения aj подсчитаем количество элементов, стоящих левее и строго
больших aj. Затем для
каждого aj подсчитаем в в
suff[j] количество элементов, стоящих
правее и строго меньших aj.
Искомое
количество троек равно
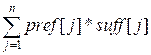
Произведение
pref[j] * suff[j] соответствует количеству искомых троек, в середине
которых стоит aj.
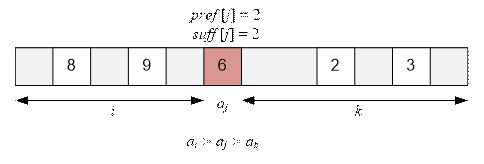
·
pref[j] = 2, так как слева от aj = 6 стоит два
числа, больших 6: 8 и 9.
·
suff[j] = 2, так как справа от aj = 6 стоит два
числа, меньших 6: 2 и 3.
Имеется pref[j] * suff[j] = 2 * 2 = 4 инвертированные
тройки, в которых aj = 6 стоит посередине: (8, 6, 2), (8, 6, 3), (9, 6, 2), (9, 6, 3).
Рассмотрим более
детально как построить массив pref[i].
Заведем массив b размером n,
изначально обнулим его. Его обработку
моделируем деревом Фенвика. На каждой итерации будем производить прибавление b[a[i]]++. Чтобы узнать количество чисел,
больших a[i], на i-ой итерации, следует вычислить сумму b[a[i] + 1] + b[a[i] + 2] + …
+ b[n]. Она в свое время равна сумме
всех чисел массива b минус сумма b[0] + b[1] + … + b[a[i]]. Сумма всех чисел в массиве b на i-ой итерации как раз
и равна количеству итераций i, поскольку
на каждой итерации мы увеличивали один из элементов b на единицу. Таким образом
pref[i] = i – (b[0] + b[1] + … + b[a[i]])
При вычислении
суффиксов также моделируем работу массива b, производя прибавление b[a[i]]++ на каждой итерации. При этом числа массива а
рассматриваем справа налево: an,
an-1, …, a1. Тогда
количество элементов, стоящих правее и строго меньших ai, равно b[0] + b[1] + … + b[a[i] – 1], что и есть
suf[i].
Пример
Рассмотрим
следующий тест:
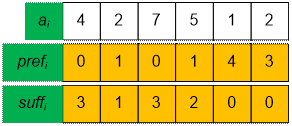
Количество
искомых троек равно
0 * 3 + 1 * 1 +
0 * 3 + 1 * 2 + 4 * 0 + 3 * 0 = 3
Рассмотрим,
например, подсчет числа инверсий ai
> aj > ak, у которых aj = 5. Их число равно pref[4] * suff[4] = 1 * 2
= 2.
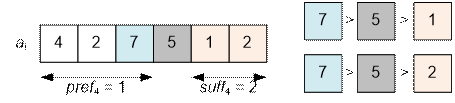
Рассмотрим
процесс вычисления массива pref.
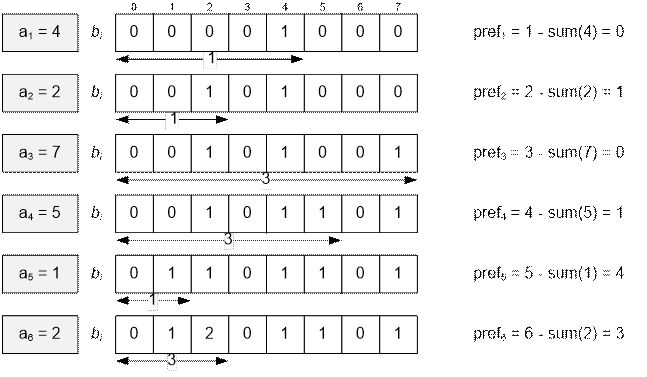
Реализация алгоритма
Объявим
глобальные массивы.
#define MAX 100010
int Fenwick[MAX], a[MAX], pref[MAX];
Вычисление суммы b[0] + b[1] + … + b[i].
int Summma0_i(int i)
{
int result = 0;
for (; i >= 0; i = (i & (i + 1)) - 1)
result +=
Fenwick[i];
return result;
}
Увеличение элемента b[i] на единицу.
void IncElement(int i)
{
for (; i < MAX; i = (i | (i+1)))
Fenwick[i]++;
}
Основная часть программы. Читаем входные данные.
scanf("%d",
&n);
for(i = 1; i <= n; ++i)
scanf("%d", &a[i]);
Для каждого
значения ai подсчитаем
количество элементов, стоящих левее и строго больших ai. Это значение занесем в pref[i].
for(i = 1; i <= n; i++)
{
IncElement(a[i]);
pref[i] = i - Summma0_i(a[i]);
}
Двигаемся справа налево по массиву a. Вычисляем результат по приведенной в анализе формуле.
memset(Fenwick,0,sizeof(Fenwick));
for(i = n; i >= 1; i--)
{
IncElement(a[i]);
res += 1LL * pref[i] * Summma0_i(a[i] - 1);
}
Выводим ответ.
printf("%lld\n",res);
Java реализация
import java.util.*;
public class Main
{
static int Fenwick[], a[], pref[];
final static int MAX = 100001;
static int Summma0_i(int i)
{
int result = 0;
for (; i >= 0; i = (i & (i + 1)) - 1)
result += Fenwick[i];
return result;
}
static void IncElement(int i)
{
for (; i < MAX; i = (i | (i+1)))
Fenwick[i]++;
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
a = new int[n+1];
pref = new int[n+1];
Fenwick = new int[MAX];
for(int i = 1; i <= n; i++)
a[i] = con.nextInt();
for(int i = 1; i <= n; i++)
{
IncElement(a[i]);
pref[i] = i - Summma0_i(a[i]);
}
Fenwick = new int[MAX];
long res = 0;
for(int i = n; i >= 1; i--)
{
IncElement(a[i]);
res += 1L * pref[i] * Summma0_i(a[i] - 1);
}
System.out.println(res);
con.close();
}
}